Gradient Descent#
import 需要的套件。一般都會全部放在程式的最前面。
import pandas as pd
配合課程說明的案例,用python演示一次。
首先定義需要的function如下:
定義模型(簡單線性迴歸):參數是截距項、斜率,及模型的input(feature),輸出是對應的模型預測值。
def model(a, b, x):
y_hat = a + b * x
return y_hat
計算損失 & gradient:計算給定參數時(即當前模型)的損失值 & gradient。
def get_loss(data, a, b):
loss = 0
for i in range(0, data.shape[0]):
x, y = data['x'][i], data['y'][i]
loss += ( y - model(a, b, x))**2
return loss
def get_gradient(data, a, b):
gradient = 0
for i in range(0, data.shape[0]):
x, y = data['x'][i], data['y'][i]
gradient += -2 * ( y - model(a, b, x))
return gradient
更新參數:根據輸入的gradient,以及給定的learning rate(lr),將目前的參數值更新為新的參數值。
def update_param(param, gradient, lr):
new_param = param - gradient * lr
return new_param
定義與課程說明相同的資料如下:
data = pd.DataFrame({
'x': [0.5, 2.3, 2.9],
'y': [1.4, 1.9, 3.2]
})
用graident descent更新截距項#
與課程說明相同,假設僅更新截距項。
# step 1: 隨機取值。
a = 0
# 初始化一些variable,供後續繪圖使用。
graph_a = []
graph_loss = []
for i in range(0, 50): # 假設僅迭代50次。
print(f'>>> iteration: {i}')
# step 2: 計算gradient。
gradient = get_gradient(data=data, a=a, b=0.64)
print(f'gradient = {gradient:.4f}')
# step 3: 更新參數
a = update_param(param=a, gradient=gradient, lr=0.1)
print(f'a = {a:.4f}')
# 儲存每一次迭代時的截距項,供繪圖用。
graph_a.append(a)
# 儲存並計算每一次迭代時的損失,供繪圖用。
loss = get_loss(data=data, a=a, b=0.64)
graph_loss.append(loss)
print(f'loss: {loss:.4f}\n')
>>> iteration: 0
gradient = -5.7040
a = 0.5704
loss: 0.8784
>>> iteration: 1
gradient = -2.2816
a = 0.7986
loss: 0.5140
>>> iteration: 2
gradient = -0.9126
a = 0.8898
loss: 0.4557
>>> iteration: 3
gradient = -0.3651
a = 0.9263
loss: 0.4464
>>> iteration: 4
gradient = -0.1460
a = 0.9409
loss: 0.4449
>>> iteration: 5
gradient = -0.0584
a = 0.9468
loss: 0.4447
>>> iteration: 6
gradient = -0.0234
a = 0.9491
loss: 0.4446
>>> iteration: 7
gradient = -0.0093
a = 0.9500
loss: 0.4446
>>> iteration: 8
gradient = -0.0037
a = 0.9504
loss: 0.4446
>>> iteration: 9
gradient = -0.0015
a = 0.9506
loss: 0.4446
>>> iteration: 10
gradient = -0.0006
a = 0.9506
loss: 0.4446
>>> iteration: 11
gradient = -0.0002
a = 0.9507
loss: 0.4446
>>> iteration: 12
gradient = -0.0001
a = 0.9507
loss: 0.4446
>>> iteration: 13
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 14
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 15
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 16
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 17
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 18
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 19
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 20
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 21
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 22
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 23
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 24
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 25
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 26
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 27
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 28
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 29
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 30
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 31
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 32
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 33
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 34
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 35
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 36
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 37
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 38
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 39
gradient = -0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 40
gradient = 0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 41
gradient = 0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 42
gradient = 0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 43
gradient = 0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 44
gradient = 0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 45
gradient = 0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 46
gradient = 0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 47
gradient = 0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 48
gradient = 0.0000
a = 0.9507
loss: 0.4446
>>> iteration: 49
gradient = 0.0000
a = 0.9507
loss: 0.4446
graph_df = pd.DataFrame({'a': graph_a, 'loss': graph_loss})
graph_df.plot.scatter(x='a', y='loss')
<Axes: xlabel='a', ylabel='loss'>
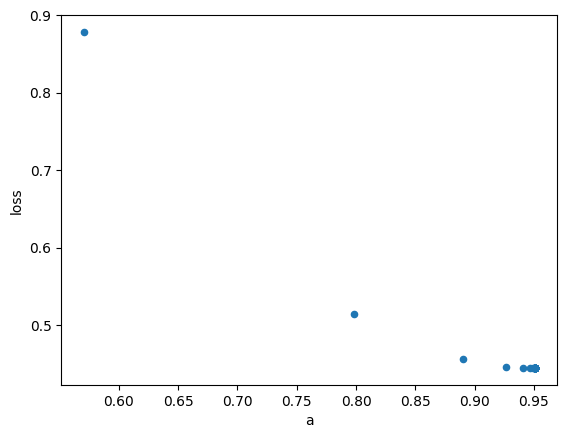
可以看到上圖顯示,迭代了50次之後,截距項從0逐漸移動至0.95附近。
用graident descent更新截距項 & 斜率#
接著,下面的程式示範了如何同時更新截距項 & 斜率。
def get_gradients(data, a, b):
gradient_a = 0
gradient_b = 0
for i in range(0, data.shape[0]):
x, y = data['x'][i], data['y'][i]
gradient_a += -2 * ( y - model(a, b, x))
gradient_b += -2 * x * ( y - model(a, b, x))
return gradient_a, gradient_b
# step 1: 隨機取值。
a = 0
b = 1
# 初始化一些variable,供後續繪圖使用。
graph_a = []
graph_b = []
graph_loss = []
for i in range(0, 701):
# step 2: 計算gradient。
gradient_a, gradient_b = get_gradients(data=data, a=a, b=b)
# step 3: 更新參數
a = update_param(param=a, gradient=gradient_a, lr=0.01)
b = update_param(param=b, gradient=gradient_b, lr=0.01)
# 儲存每一次迭代時的截距項,供繪圖用。
graph_a.append(a)
graph_b.append(b)
# 儲存並計算每一次迭代時的損失,供繪圖用。
loss = get_loss(data=data, a=a, b=b)
graph_loss.append(loss)
# 因為迭代的次數較多,讓程式每迭代10次才print內容。
if i % 10 == 0:
print(f'>>> iteration: {i}')
print(f'gradient_a = {gradient_a:.4f}, gradient_b = {gradient_b:.4f}')
print(f'a = {a:.4f}, b = {b:.4f}')
print(f'loss: {loss:.4f}')
print('')
>>> iteration: 0
gradient_a = -1.6000, gradient_b = -0.8000
a = 0.0160, b = 1.0080
loss: 1.0311
>>> iteration: 10
gradient_a = -0.9601, gradient_b = 0.3810
a = 0.1269, b = 0.9906
loss: 0.9005
>>> iteration: 20
gradient_a = -0.8470, gradient_b = 0.3603
a = 0.2163, b = 0.9531
loss: 0.8068
>>> iteration: 30
gradient_a = -0.7549, gradient_b = 0.3216
a = 0.2958, b = 0.9192
loss: 0.7324
>>> iteration: 40
gradient_a = -0.6729, gradient_b = 0.2867
a = 0.3667, b = 0.8890
loss: 0.6733
>>> iteration: 50
gradient_a = -0.5998, gradient_b = 0.2556
a = 0.4299, b = 0.8621
loss: 0.6263
>>> iteration: 60
gradient_a = -0.5347, gradient_b = 0.2278
a = 0.4863, b = 0.8381
loss: 0.5890
>>> iteration: 70
gradient_a = -0.4766, gradient_b = 0.2031
a = 0.5365, b = 0.8167
loss: 0.5594
>>> iteration: 80
gradient_a = -0.4249, gradient_b = 0.1810
a = 0.5812, b = 0.7976
loss: 0.5358
>>> iteration: 90
gradient_a = -0.3787, gradient_b = 0.1614
a = 0.6212, b = 0.7806
loss: 0.5171
>>> iteration: 100
gradient_a = -0.3376, gradient_b = 0.1438
a = 0.6567, b = 0.7654
loss: 0.5022
>>> iteration: 110
gradient_a = -0.3009, gradient_b = 0.1282
a = 0.6884, b = 0.7519
loss: 0.4904
>>> iteration: 120
gradient_a = -0.2683, gradient_b = 0.1143
a = 0.7167, b = 0.7399
loss: 0.4810
>>> iteration: 130
gradient_a = -0.2391, gradient_b = 0.1019
a = 0.7419, b = 0.7291
loss: 0.4735
>>> iteration: 140
gradient_a = -0.2132, gradient_b = 0.0908
a = 0.7644, b = 0.7196
loss: 0.4676
>>> iteration: 150
gradient_a = -0.1900, gradient_b = 0.0810
a = 0.7844, b = 0.7110
loss: 0.4629
>>> iteration: 160
gradient_a = -0.1694, gradient_b = 0.0722
a = 0.8022, b = 0.7034
loss: 0.4591
>>> iteration: 170
gradient_a = -0.1510, gradient_b = 0.0643
a = 0.8181, b = 0.6967
loss: 0.4561
>>> iteration: 180
gradient_a = -0.1346, gradient_b = 0.0573
a = 0.8323, b = 0.6906
loss: 0.4538
>>> iteration: 190
gradient_a = -0.1200, gradient_b = 0.0511
a = 0.8450, b = 0.6852
loss: 0.4519
>>> iteration: 200
gradient_a = -0.1069, gradient_b = 0.0456
a = 0.8562, b = 0.6804
loss: 0.4504
>>> iteration: 210
gradient_a = -0.0953, gradient_b = 0.0406
a = 0.8663, b = 0.6762
loss: 0.4492
>>> iteration: 220
gradient_a = -0.0850, gradient_b = 0.0362
a = 0.8752, b = 0.6723
loss: 0.4483
>>> iteration: 230
gradient_a = -0.0758, gradient_b = 0.0323
a = 0.8832, b = 0.6689
loss: 0.4475
>>> iteration: 240
gradient_a = -0.0675, gradient_b = 0.0288
a = 0.8903, b = 0.6659
loss: 0.4469
>>> iteration: 250
gradient_a = -0.0602, gradient_b = 0.0256
a = 0.8967, b = 0.6632
loss: 0.4464
>>> iteration: 260
gradient_a = -0.0537, gradient_b = 0.0229
a = 0.9023, b = 0.6608
loss: 0.4461
>>> iteration: 270
gradient_a = -0.0478, gradient_b = 0.0204
a = 0.9073, b = 0.6587
loss: 0.4458
>>> iteration: 280
gradient_a = -0.0426, gradient_b = 0.0182
a = 0.9118, b = 0.6567
loss: 0.4455
>>> iteration: 290
gradient_a = -0.0380, gradient_b = 0.0162
a = 0.9158, b = 0.6550
loss: 0.4453
>>> iteration: 300
gradient_a = -0.0339, gradient_b = 0.0144
a = 0.9194, b = 0.6535
loss: 0.4452
>>> iteration: 310
gradient_a = -0.0302, gradient_b = 0.0129
a = 0.9226, b = 0.6522
loss: 0.4451
>>> iteration: 320
gradient_a = -0.0269, gradient_b = 0.0115
a = 0.9254, b = 0.6509
loss: 0.4450
>>> iteration: 330
gradient_a = -0.0240, gradient_b = 0.0102
a = 0.9280, b = 0.6499
loss: 0.4449
>>> iteration: 340
gradient_a = -0.0214, gradient_b = 0.0091
a = 0.9302, b = 0.6489
loss: 0.4448
>>> iteration: 350
gradient_a = -0.0191, gradient_b = 0.0081
a = 0.9322, b = 0.6481
loss: 0.4448
>>> iteration: 360
gradient_a = -0.0170, gradient_b = 0.0072
a = 0.9340, b = 0.6473
loss: 0.4448
>>> iteration: 370
gradient_a = -0.0152, gradient_b = 0.0065
a = 0.9356, b = 0.6466
loss: 0.4447
>>> iteration: 380
gradient_a = -0.0135, gradient_b = 0.0058
a = 0.9370, b = 0.6460
loss: 0.4447
>>> iteration: 390
gradient_a = -0.0120, gradient_b = 0.0051
a = 0.9383, b = 0.6455
loss: 0.4447
>>> iteration: 400
gradient_a = -0.0107, gradient_b = 0.0046
a = 0.9394, b = 0.6450
loss: 0.4447
>>> iteration: 410
gradient_a = -0.0096, gradient_b = 0.0041
a = 0.9404, b = 0.6446
loss: 0.4447
>>> iteration: 420
gradient_a = -0.0085, gradient_b = 0.0036
a = 0.9413, b = 0.6442
loss: 0.4447
>>> iteration: 430
gradient_a = -0.0076, gradient_b = 0.0032
a = 0.9421, b = 0.6438
loss: 0.4446
>>> iteration: 440
gradient_a = -0.0068, gradient_b = 0.0029
a = 0.9429, b = 0.6435
loss: 0.4446
>>> iteration: 450
gradient_a = -0.0060, gradient_b = 0.0026
a = 0.9435, b = 0.6433
loss: 0.4446
>>> iteration: 460
gradient_a = -0.0054, gradient_b = 0.0023
a = 0.9441, b = 0.6430
loss: 0.4446
>>> iteration: 470
gradient_a = -0.0048, gradient_b = 0.0020
a = 0.9446, b = 0.6428
loss: 0.4446
>>> iteration: 480
gradient_a = -0.0043, gradient_b = 0.0018
a = 0.9450, b = 0.6426
loss: 0.4446
>>> iteration: 490
gradient_a = -0.0038, gradient_b = 0.0016
a = 0.9454, b = 0.6424
loss: 0.4446
>>> iteration: 500
gradient_a = -0.0034, gradient_b = 0.0014
a = 0.9458, b = 0.6423
loss: 0.4446
>>> iteration: 510
gradient_a = -0.0030, gradient_b = 0.0013
a = 0.9461, b = 0.6421
loss: 0.4446
>>> iteration: 520
gradient_a = -0.0027, gradient_b = 0.0012
a = 0.9464, b = 0.6420
loss: 0.4446
>>> iteration: 530
gradient_a = -0.0024, gradient_b = 0.0010
a = 0.9466, b = 0.6419
loss: 0.4446
>>> iteration: 540
gradient_a = -0.0021, gradient_b = 0.0009
a = 0.9469, b = 0.6418
loss: 0.4446
>>> iteration: 550
gradient_a = -0.0019, gradient_b = 0.0008
a = 0.9471, b = 0.6417
loss: 0.4446
>>> iteration: 560
gradient_a = -0.0017, gradient_b = 0.0007
a = 0.9472, b = 0.6417
loss: 0.4446
>>> iteration: 570
gradient_a = -0.0015, gradient_b = 0.0006
a = 0.9474, b = 0.6416
loss: 0.4446
>>> iteration: 580
gradient_a = -0.0014, gradient_b = 0.0006
a = 0.9475, b = 0.6415
loss: 0.4446
>>> iteration: 590
gradient_a = -0.0012, gradient_b = 0.0005
a = 0.9477, b = 0.6415
loss: 0.4446
>>> iteration: 600
gradient_a = -0.0011, gradient_b = 0.0005
a = 0.9478, b = 0.6414
loss: 0.4446
>>> iteration: 610
gradient_a = -0.0010, gradient_b = 0.0004
a = 0.9479, b = 0.6414
loss: 0.4446
>>> iteration: 620
gradient_a = -0.0009, gradient_b = 0.0004
a = 0.9480, b = 0.6413
loss: 0.4446
>>> iteration: 630
gradient_a = -0.0008, gradient_b = 0.0003
a = 0.9481, b = 0.6413
loss: 0.4446
>>> iteration: 640
gradient_a = -0.0007, gradient_b = 0.0003
a = 0.9481, b = 0.6413
loss: 0.4446
>>> iteration: 650
gradient_a = -0.0006, gradient_b = 0.0003
a = 0.9482, b = 0.6412
loss: 0.4446
>>> iteration: 660
gradient_a = -0.0005, gradient_b = 0.0002
a = 0.9483, b = 0.6412
loss: 0.4446
>>> iteration: 670
gradient_a = -0.0005, gradient_b = 0.0002
a = 0.9483, b = 0.6412
loss: 0.4446
>>> iteration: 680
gradient_a = -0.0004, gradient_b = 0.0002
a = 0.9483, b = 0.6412
loss: 0.4446
>>> iteration: 690
gradient_a = -0.0004, gradient_b = 0.0002
a = 0.9484, b = 0.6412
loss: 0.4446
>>> iteration: 700
gradient_a = -0.0003, gradient_b = 0.0001
a = 0.9484, b = 0.6412
loss: 0.4446
graph_df = pd.DataFrame({'a': graph_a, 'b': graph_b, 'loss': graph_loss})
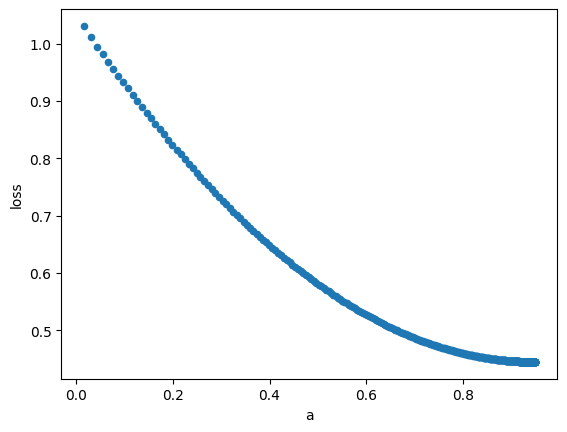
graph_df.plot.scatter(x='a', y='loss')
<Axes: xlabel='a', ylabel='loss'>
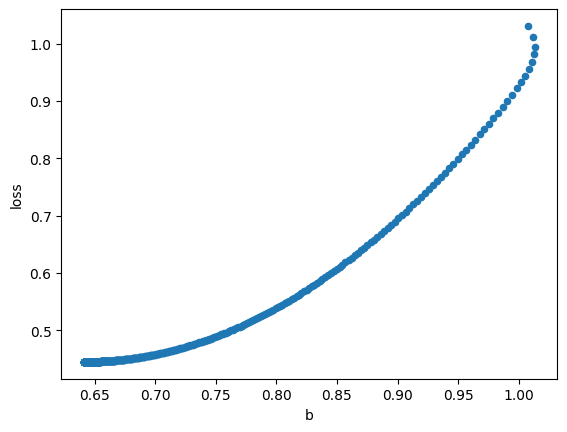
graph_df.plot.scatter(x='b', y='loss')
<Axes: xlabel='b', ylabel='loss'>
print(f'final a: {graph_a[-1]}')
print(f'final b: {graph_b[-1]}')
final a: 0.9484228728799461
final b: 0.6411513598871877
依照上面的結果,gradient descent方法,找到的a是接近0.95,b則是約0.64。
接下來測試如果使用傳統OLS方法,估計出來的數值是否接近。
OLS 結果比較#
import statsmodels.formula.api as smf
%matplotlib inline
這邊使用的套件是statsmodels,可以用類似寫方程式的方法來跑統計模型。
result = smf.ols('y ~ x', data=data).fit()
結果如下:
估計結果其實很接近gradient descent的估計方法。
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.743
Model: OLS Adj. R-squared: 0.485
Method: Least Squares F-statistic: 2.884
Date: Thu, 28 Mar 2024 Prob (F-statistic): 0.339
Time: 07:29:54 Log-Likelihood: -1.3931
No. Observations: 3 AIC: 6.786
Df Residuals: 1 BIC: 4.983
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.9487 0.814 1.165 0.451 -9.395 11.292
x 0.6410 0.377 1.698 0.339 -4.156 5.438
==============================================================================
Omnibus: nan Durbin-Watson: 2.846
Prob(Omnibus): nan Jarque-Bera (JB): 0.392
Skew: -0.470 Prob(JB): 0.822
Kurtosis: 1.500 Cond. No. 5.35
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
/Users/curtislu/Library/Caches/pypoetry/virtualenvs/ntu-ps-intro-ml-GyDE60mE-py3.11/lib/python3.11/site-packages/statsmodels/stats/stattools.py:74: ValueWarning: omni_normtest is not valid with less than 8 observations; 3 samples were given.
warn("omni_normtest is not valid with less than 8 observations; %i "
也可以使用Scikit-learn套件的LinearRegression來做到一樣的結果。
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# Creating a Linear Regression model object
model = LinearRegression()
# Fitting the model to the data (data需整理成符合規格的形狀)
model.fit(data['x'].values.reshape(-1, 1), data['y'].values)
# Once fitted, you can get the coefficients and intercept of the linear regression line
print(f"Coefficient (slope): {model.coef_}")
print(f"Intercept: {model.intercept_}")
Coefficient (slope): [0.64102564]
Intercept: 0.9487179487179489

